GNN谱图理论简述

XJTU_zsy

从代数角度分析GNN的工作原理

• GNN谱图理论简述
• 谱图理论简述
  • 1.拉普拉斯算子简述
    • 简介
    • 傅里叶级数简述
    • 思想借鉴
      • 1.定义图拉普拉斯算子
      • 2.图频域基底
  • 傅里叶变换
  • 卷积和频域
  • 对图信号处理
    • 直观理解这个公式
  • reference

谱图理论简述

从代数角度分析GNN的工作原理

1.拉普拉斯算子简述

简介

我们知道拉普拉斯算子是一个二阶微分算子，$\Delta f = \nabla ^2 f = \Delta ·\Delta f $ 我们通常在计算函数的二阶导数时用到它。

定义上看：它反映的是函数变化率的变化率。

傅里叶级数简述

可以由$\mathrm{\Delta }f=n^{2}f$这个特征方程推出一组正余弦函数$\mathcal{F}=\{1,cos(nx),sin(nx)\}$，这组函数$\mathcal{F}$构成函数$f(x)\in L_2$上的一组正交基，可以对函数$f(x)\in L_2$进行展开，也就是傅里叶级数展开。函数$f$的傅里叶级数展开可以理解为函数$f$在不同基函数下的投影，可以认为是$f$中的不同n(正余弦的频率系数)大小。

从而可以用$\varphi (n)$来描述这个函数。

显然，这个$\varphi (n)$的定义域是离散的。

进一步地，我们找到了一组基底$\mathcal{F}=\{1,cos(nx),sin(nx)\}$来描述一个函数空间$f(x)\in L_2$，使得我们对$f(x)\in L_2$的研究可以统一到一组基底上，为我们提供了一个全新的角度。

思想借鉴

1.定义图拉普拉斯算子

图$\mathcal{G}=(X,A)$,A是邻接矩阵, 用u表示节点，节点的特征信息用$x=f(u)$表示，$X=f(U)$。

离散拉普拉斯算子

${\nabla }_d^{2}f=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$

推广到图:

单个节点的拉普拉斯算子：

$$\begin{array}{r}\mathrm{\Delta }f(u_j)\\ & =\sum _{u_i\in neighbor(u_j)}f(u_j)-f(u_i)\\ & =degree(v)\times f(v)-\sum _{u_i\in neighbor(v)}f(u_i)\\ & =\sum _k{A}_{jk}\times f(u_j)-A_j\ast f(U)\\ (1)\end{array}$$

则所有节点：

$$\begin{array}{r}\mathrm{\Delta }f(U)\\ & =[\mathrm{\Delta }f(u_1)\mathrm{\Delta }f(u_2)...]\\ & =[...(\sum _k{A}_{jk}\times f(u_j)-A_j\ast f(U))...]\\ & =[...(\sum _k{A}_{jk}\times f(u_j))...]-A\ast f(U)\\ & =D\ast f(U)-A\ast f(U)\\ & =(D-A)\ast f(U)\\ (2)\end{array}$$

其中D是度对角阵。*表示通常意义的内积。

2.图频域基底

记$\overline{A}=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}$其中$D^{-\frac{1}{2}}$为了对称归一化，显然$\overline{A}$是一个实对称矩阵，$\lambda \overrightarrow{x}=\overline{A}\overrightarrow{x}$可以求出它的|U|个特征向量和对应的非负特征值，这几个特征向量$\mathcal{VEC}=\{\overrightarrow{v_1},...\}$就构成了可以描述这个图的拓扑结构的基底，记$V^T$的列为$v_i$:

$$\begin{gathered} \overline{A}=V\mathrm{\Lambda }{V}^T \\ (3) \end{gathered}$$

傅里叶变换

在傅里叶级数的基础上，用复数欧拉公式可以较为容易推导出傅里叶变换为：

$$\begin{gathered} F(\omega )=F(f(t))={\int }_{-\infty }^{+\infty }f(t)e^{-j\omega t}dt \\ (4) \end{gathered}$$

就是把上面傅里叶级数的n从整数变到w实数范围以后，将原函数对各个基底作投影。

类似的：

定义图上傅里叶变换

$$\begin{gathered} F(u_i)=F(f(u_i))=V{x}_i \\ (5) \end{gathered}$$

逆变换

$$\begin{gathered} f(u_i)=F^{-1}(F(u_i))=V^{T}V{x}_i \\ (6) \end{gathered}$$

卷积和频域

卷积：单位脉冲函数和原函数卷积为原函数

信号处理：时不变系统中，处理作用于原函数，相当于处理作用于单位脉冲函数后和原函数卷积

卷积和频域：时域卷积等于频域相乘后逆变换。

对图信号处理

冲击函数在图上就是每个节点施加一个constant([1,1,1....])。

在$\mathcal{H}()$下图信号X的输出Y，则：

$$\begin{array}{r}Y\\ & =V^T((V{\mathcal{H}}_{\mathcal{0}}(\mathrm{\Lambda }))(VX)),\\ \\ & \mathrm{把}V{\mathcal{H}}_{\mathcal{0}}()\mathrm{并}\mathrm{为}\mathcal{H}()\\ \\ & =V^T((\mathcal{H}(\mathrm{\Lambda }))(VX))\\ (7)\end{array}$$

对$\mathcal{H}(\mathrm{\Lambda })$作切比雪夫展开：

$$\begin{gathered} \mathcal{H}(\mathrm{\Lambda })\approx \sum _{i=0}^K{\theta }_i{T}_k(\hat{\mathrm{\Lambda }})， \\ \hat{\mathrm{\Lambda }}=\frac{2\mathrm{\Lambda }}{{\lambda }_{max}}-I_N\mathrm{是}\mathrm{为}\mathrm{了}\mathrm{满}\mathrm{足}\mathrm{切}\mathrm{比}\mathrm{雪}\mathrm{夫}\mathrm{展}\mathrm{开}\mathrm{的}\mathrm{条}\mathrm{件} \\ (8) \end{gathered}$$

用一阶近似并取得${\lambda }_{max}=2$(切比雪夫多项式$Tk$取$Tk(x)={\theta }_0+{\theta }_{1}x$)：

$$\begin{array}{r}Y\\ & \mathrm{代}\mathrm{入}(7)(8)\\ & ={\theta }_{0}X+{\theta }_1{V}^T((\mathrm{\Lambda }-I_N)(VX))\\ & ={\theta }_{0}X-{\theta }_1(D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}X)\\ & \mathrm{令}\theta ={\theta }_0=-{\theta }_1\mathrm{则}:\\ & =\theta ((D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}+I_N)X)\\ & \mathrm{将}{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}+I_N\mathrm{归}\mathrm{一}\mathrm{化}\mathrm{到}[0,1]:\\ & =\theta ((({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}))X)\\ & \mathrm{总}\mathrm{体}\mathrm{来}\mathrm{看}，\\ & D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}-->{\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}},\hat{A}=A+I_N,\widehat{D_{ii}}=\sum _j\widehat{A_{ij}}\\ (9)\end{array}$$

最后加上激活函数得到了单层GCN：

$$Y=\sigma (({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}})HW)$$

直观理解这个公式

聚合邻居节点的信息。

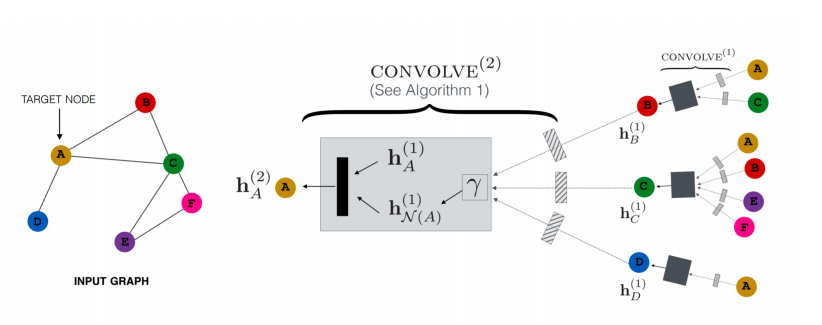
reference

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering

https://doi.org/10.48550/arXiv.1606.09375

CS224W | Home (stanford.edu)

GNN入门之路: 01.图拉普拉斯矩阵的定义、推导、性质、应用 - 知乎 (zhihu.com)